May 2014
Blog 12-2 | June 2014 | April 2014

Wellenausbreitung: Zeiger, Welle und Gleichung

26/05/14 17:34

1. Hinweise zum Abitur (s. auch Liste Zentrale Versuche)

2. Verschiedene Möglichkeiten, die Ausbreitung einer Welle zu veranschaulichen (in GeoGebra): Oszillatorenkette_03-2
a) über die Schwingungen einzelner Oszillatoren (-> blaue Balken)
b) über die Kreisbewegung der den Schwingungen zugeordneten Zeiger (-> blaue Pfeile)
c) über den Graphen der Sinusfunktion (harmonische Welle).

3. Übung -> Arbeitsblatt: WellenausbreitungZeiger

4. Vertiefung -> Übung 8, Aufgabe 1
b) Foto, räumliche Periodizität
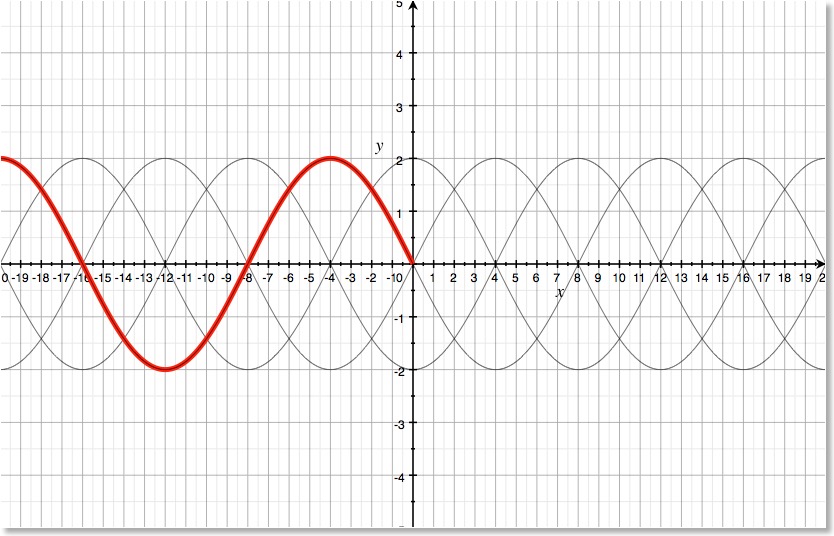
Welle1
Die (rote) Welle ( Lambda: 16) steht zum Zeitpunkt t = 0 noch links von x = 0. Je nach verstrichener Zeit wandert sie entsprechend nach rechts,
z. B. ist sie zum Zeitpunkt t = T/4 gerade bis zur Stelle x = 4 gekommen.

c) Film, zeitliche Periodizität
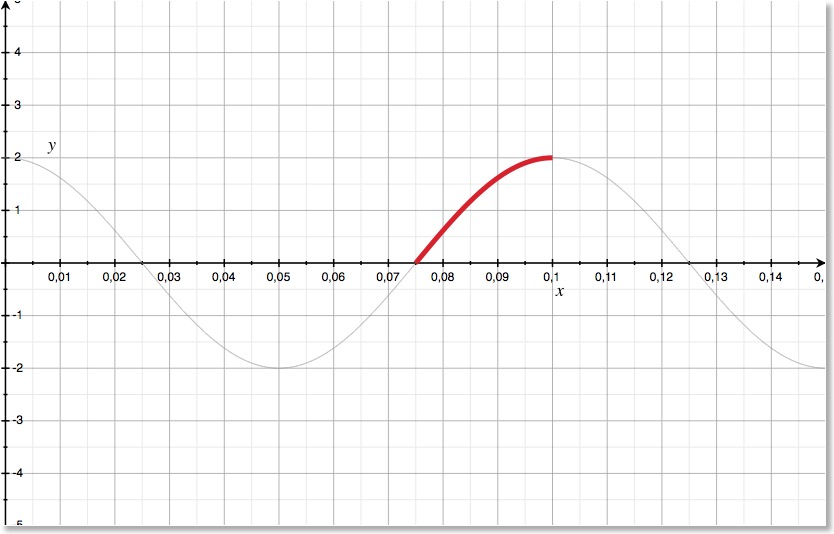
Welle3
Die Welle ( Lambda: 16, T = 0,1) ist erst zum Zeitpunkt t = 3T/4 an der Stelle x = 12 angekommen. Erst ab diesem Zeitpunkt schwingt der Oszillator an dieser Stelle.

Smart zu 4.: 26-05-14

ITECH-Projekt

16/05/14 15:16

Vorbereitungen zum Workshop für den 9. Jahrgang: siehe Extra-Ordner 12-2 ITECH3

Die harmonische Welle - mathematische Betrachtung

12/05/14 19:15

1. Veranschaulichung von Wellen (2D, 1D): http://phet.colorado.edu/en/simulation/wave-interference

2. Die harmonische Welle
a) Kennzeichen von harmonischer Schwingung und harmonischer Welle
b) Ausbreitungsgeschwindigkeit und Wellengleichung

http://www.familie-michele.de/gis/material11/Wellen_und_Zeiger.html

Arbeitsblatt: Wellenausbreitung im Zeigermodell


3. Übung 8: Aufgabe 1 (Lösung siehe 26.05.)

Hannes Protokoll:

Smart: 12-05-14

Schwingung oder Welle?

11/05/14 11:02

1. Übung 8a: Aufgabe 2

2. Zuordnung: Schwingung oder Welle?

WelleLaOla

3. Kennzeichen zur Unterscheidung Schwingung/Welle

Arthur Protokoll: ProtokollArthur2

Smart: 09-05-14

Das Fadenpendel

07/05/14 17:12

1. Faktoren, die die Schwingungsdauer beeinflussen könnten

2. Versuchsreihe: Änderung der Länge -> Von den Messwerten zum funktionellen Zusammenhang
Fadenpendel
3. Versuchsreihe: Änderung der Masse

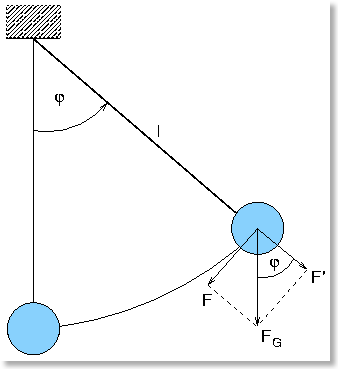
4. Theoretische Herleitung des funktionellen Zusammenhangs über den Vergleich von Federschwinger und Fadenpendel
Fadenpendel2




Clemens Protokoll: ProtokollClemens2

Der harmonische Oszillator – mathematische Betrachtung

05/05/14 16:58

1. Harmonische Oszillatoren: Federschwinger – Fadenpendel – Schwingkreis

http://www.walter-fendt.de/ph14d/federpendel.htm

http://www.walter-fendt.de/ph14d/fadenpendel.htm

http://www.walter-fendt.de/ph14d/schwingkreis.htm


2. Vom Energieerhaltungssatz zur Differentialgleichung der harmonischen Schwingung

3. Analogiebetrachtung von Kreisbewegung und Federschwinger -> Herleitung der Bewegungsgleichung der harmonischen Schwingung: Mathematische Beschreibung der harmonischen Schwingung

http://www.geogebra.org/de/upload/files/dynamische_arbeitsblaetter/lwolf/kreisbewegung/kreisprojektion.html

4. Übungsaufgaben 8a: Aufgabe 1

Smart: 05-05-14

Alex Protokoll: